Towers of Hanoi Recursive Ananlysis

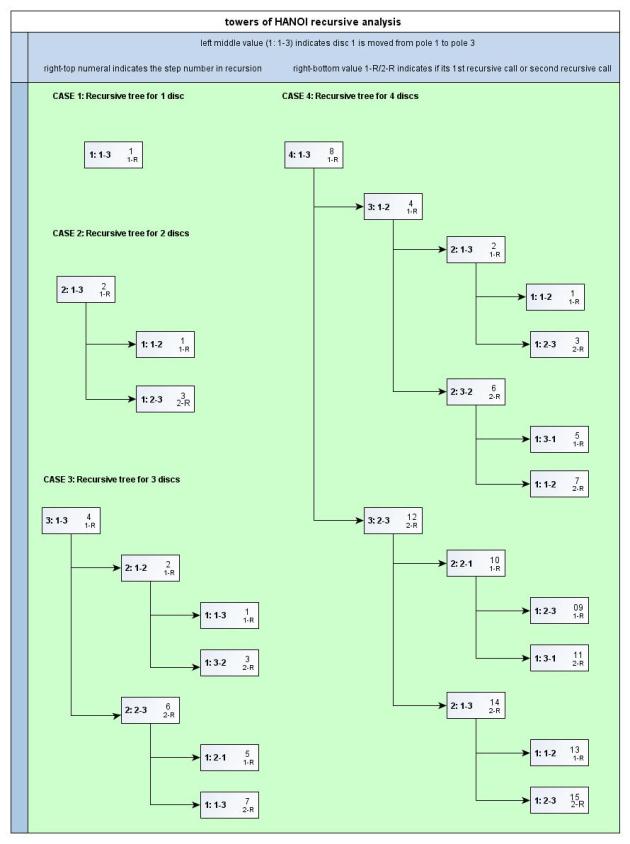
Recursive program to towers of hanoi problem

package algorithms.recursion;

/**
 * @author ntallapa
 *
 */
public class TowersOfHanoi {
	
	/**
	 * This recursive algorithm takes (2^n-1) iterations to complete the task
	 * 
	 * @param n number of disks
	 * @param startPole
	 * @param endPole
	 */
	public static void move(int n, int startPole, int endPole) {
		if (n== 0){
			return; 
		}
		// here 6 is summation of poles, i.e, sigma(3) = 3+2+1 = 6
		int intermediatePole = 6 - startPole - endPole;
		
		// Move n–1 disks from disk 1 to disk 2, using disk 3 as a temporary holding area.
		move(n-1, startPole, intermediatePole);
		
		// Move the last disk (the largest) from disk 1 to disk 3.
		System.out.println("Move " +n + " from " + startPole + " to " +endPole);
		
		//  Move n–1 disks from disk 2 to disk 3, using disk 1 as a temporary holding area.
		move(n-1, intermediatePole, endPole);
	}
	
	public static void main(String[] args) {
		move(4, 1, 3);
	}	
}

For 2 discs we need 3 iterations, 3 discs we need 7 iterations, 4 discs we need 15 iterations, etc… from this it can be realized that to move ‘n’ discs we need (2^n)-1 iterations.