Understanding quicksort algorithm
September 17, 2013 3 Comments
I see many people finding it very difficult to remember this algorithm, so is this article. Complete source code with few unit tests can be downloaded here
To put it in a simple way, Quicksort algorithm is as simple as this diagram depicts.
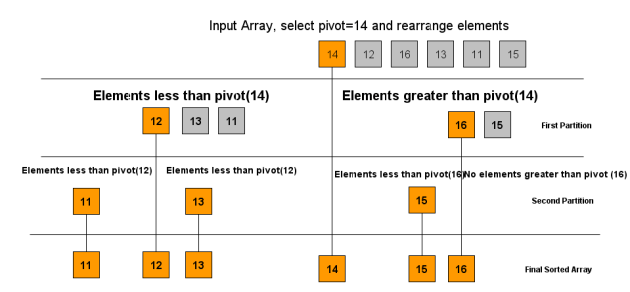
Explanation of the above diagram: Every time we are choosing first element as the pivot and making the partition, i.e, elements less than pivot comes to left partition and vice versa. And in what order these elements should be brought into left and right partitions is explained in partition logic below. And partitioning itself is a recursive mechanism we do that as part of actual quicksort logic.
Note: Just because this algorithm is in_place algorithm you might find it bit confusing(but efficient), but otherwise if you choose simplicity you can always implement it in other ways.
Complexity of Quicksort Algorithm: On an average Quicksort Algorithm has the complexity of O(nlogn) and in the worst case it has O(n^2) when the elements of the input array are sorted (ascending or descending order). It is an in place algorithm in the sense it does not takes any additional space.
It is a divide and conquer algorithm where we partition the given array with respect to a particular element(called as ‘PIVOT’) such that the lower partition elements of the array are less than the pivot and upper partition elements of the array are higher than the pivot.
Concept of Partition and Pivot:
Rule of Pivot: There is not any rule of pivot as such but it can be any element of the given array, here I am considering the first element as the pivot in every partition. How choosing of an pivot effects the distribution of the elements in partitioning and its role in the complexity of the quicksort logic will be discussed in future posts.
Rule of Partition: The lower partition should be less than the pivot and upper partition should be higher than the pivot. Running time of partition logic is linear.
Let us take an example array {14,12,16,13,11}
First Iteration: Lets say pivot is always the first element of the array(i.e, 14 in this case);
---------------------------
14 | 12 | 16 | 13 | 11 --> (a[0] is not less than pivot, hence i is stopped
--------------------------- at index 0; a[4] is not greater than pivot,hence
j is stopped at index 5. Now swap a[0] and a[4])
---------------------------
11 | 12 | 16 | 13 | 14 --> (a[2] is not less than pivot, hence i is stopped
--------------------------- at index 2; a[3] is not greater than pivot,hence
j is stopped at index 3. Now swap a[2] and a[3].)
---------------------------
11 | 12 | 13 | 16 | 14
---------------------------
0 | 1 | 2 | 3 | 4 --> Index
---------------------------
At this point index i points to 3 and j points to 2 and since i > j,
partition logic will exit resulting into two partitions
----------
Left Partition: 14 | 12
---------------
Right Partition: 13 | 16 | 11
---------------
Partition logic implemented in Java
/**
* Partition logic
*
* @param a array to be modified based on pivot
* @param left lower bound of the array
* @param right upper bound of the array
* @return the partition index where elements to its left are less than it and
* elements to its right are more than it
*/
public int partition(int[] a, int left, int right) {
// Get the pivot element
int pivot = a[left];
// Break when left is > right
while(left < = right) {
//increment the lower bound till you find the element more than the pivot
while(a[left] < pivot)
left++;
//decrement the upper bound till you find the element less than the pivot
while(a[right] > pivot)
right--;
// swap the values which are left by lower and upper bounds
if(left < = right) {
int tmp = a[left];
a[left] = a[right];
a[right] = tmp;
//increment left index and decrement right index
left++;
right--;
}
}
return left;
}
Running time of quick sort logic depends on the distribution of elements across the partitions.
Quicksort Logic:
Quicksort Logic is straight forward with couple of recursive calls. Quicksort implementation in java is shown below
/**
* Recursive quicksort logic
* @param a input array
* @param i start index of the array
* @param j end index of the array
*/
public void recursiveQuickSort(int[] a, int i, int j) {
// Handle logic to divide the array
int idx = partition(a, i, j);
// Recursively call quick sort with left part of the divided array
if(i < idx-1) {
recursiveQuickSort(a, i, idx-1);
}
// Recursively call quick sort with right part of the divided array
if(j > idx) {
recursiveQuickSort(a, idx, j);
}
}
First recursive call ‘recursiveQuickSort(a, i, idx-1);’ picks the left partition of the array and repeats the process. And second recursive call ‘recursiveQuickSort(a, idx, j);’ picks the right partition of the array and repeats the process.
Since we are returning index ‘left’, i.e, i=2 from partition() method first recursive call ‘recursiveQuickSort(a, i, idx-1);’ would consider left partition array from index 0 to 1
----------
Left Partition: 14 | 12
----------
Second recursive call ‘recursiveQuickSort(a, idx, j);’ would consider right partition array from index 2 to 4
---------------
Right Partition: 13 | 16 | 11
---------------
Complete source code with few unit tests can be downloaded here
The title “elements less than pivot(12)” in the place where you have 13 should say “elements GREATER than pivot(12)”
result:
[11, 12, 13, 16, 14, 15]
index 3 value 16
Your partition sort does NOT work.
I suggest you learn to program?
You might have passed wrong indexes to the algorithm (I explained diagram with 6 values and explanation with 5 values). Instead of
recursiveQuickSort(a, 0, 5)
you might have passed
recursiveQuickSort(a, 0, 4)
The same code is checked into git with some unit tests
https://github.com/ntallapa12/java_algos/blob/master/src/main/java/com/forum/java/algos/QuickSort.java
I would suggest you to go through it once again properly.